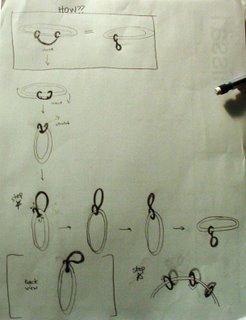
The puzzle is in this picture. How can the two shapes in the box in the upper left be the same? Topologically speaking, they are *not different*.
So how does that work? You could look at my drawing, but it sucks, so I made a video of how you convert between one shape and the other using silly putty. The rules: you can't break anything, or disconnect and reconnect anything, and there must always be the same number of holes in the object you are manipulating (in this case, it's a double-holed donut). You are allowed to stretch and shrink the material as much as you want as long as you don't change the fundamental properties of the shape.
Video is here!

4 comments:
Hi Lissa! Cool video! I hope you don't mind a few topological details :)
Actually, what you say is not technically true --- the shapes you have are different topologically. However, the reason that it's not true is actually pretty interesting!
The fundamental question here comes down to asking if there is any difference between the shapes of a figure 8 and of a theta. That is, is there any difference between a circle with two sides connected by a single point and a circle with two sides connected by a line. You can think of what you're doing to be turning a o-o shape into an 8 and then into a theta (and then back); most of what I'm about to say about 8 vs theta applies similarly to o-o vs 8, but that doesn't have a nice name :)
The technical term for "topologically the same" is "homeomorphic". Essentially, it means that for every point in one shape, there is exactly one point in the other shape that corresponds to it (and vice versa). The issue with 8 vs theta is there are a lot of points in the theta (the entire center line) that you'd want to "correspond" to the single center point in the 8. So it turns out that they are not homeomorphic.
Another way to see this is to look at "topological properties". These are properties that any pair of things which are homeomorphic must have in common. For example, connectedness --- if one thing is "just one piece", and another thing is more than one piece, then they can't be homeomorphic. In this case, both the 8 and the theta are connected. However, 8 has the property that if you take away a single point (the center point) it is no longer connected --- you can't get from the top to the bottom without going through the middle. On the other hand, a theta has no such point: no matter what point you take away, it'll still be connected. This is a topological property (you'll have to trust me on this) so these two shapes are not homeomorphic --- they are not the same topologically.
(Exercise: come up with a topological property that o-o has and 8 doesn't... this time, both of them have a point whose removal disconnects the space, so it's not exactly the same issue...)
But! All is not lost! It turns out that there's a second kind of equivalence in topology, called "homotopy equivalence", under which 8 and theta are the same! Homotopy equivalence (which is not the default kind of "the same" in topology) basically tries to capture the idea of squishing and pulling --- the idea that a line of stuff can be compressed down to a point, or that a point can be stretched out into a 46-dimensional hypercube. Any two things that are homeomorphic must be homotopy equivalent, but as we've just learned, the converse is not true. (And this isn't totally obvious --- I found it to be tough to understand at first when I learned about it; your video would have been way helpful!)
So, here's the interesting part. Do you remember the news from a month or two ago about "crazy reclusive Russian proves major conjecture"? You know now enough to understand what he proved! Here's the idea --- in math we talk about n-dimensional spheres: a circle is a 1-sphere, a basketball is a 2-sphere, Einstein claims we live in a 3-sphere, and so on. If you zoom in on a piece of a 1-sphere (a circle), it looks like a little bit of 1-dimensional space (a line). If you zoom in on a piece of a 2-sphere (basketball), it looks like a little bit of 2-dimensional space (a plane). In general, we have a concept called an "n-manifold" which is something that if you zoom in on it looks like n-dimensional space.
What the Poincare Conjecture claims is that if you have two n-manifolds (well, n-manifolds that don't go off infinitely far in some direction), and they are homotopy equivalent, then they are in fact homeomorphic. So what does that mean?
Let's say you have an n-dimensional manifold made out of Silly Putty. And let's say that you (or some hyperdimensional Lissa) made a video of yourself smooshing it into an n-sphere. And let's say you then posted on your blog "this shows that the shape I made is not topologically different from an n-sphere".
What the Poincare conjecture claims is that no annoying housemate of yours can pop up and post a page-long comment saying that you're wrong :)
Thanks Dave! Wow! I'd better get my story straight!
A couple of amendments:
First off, my statement of the Poincare conjecture was a bit off. It's not about arbitrary pairs of n-manifolds: it's about pairs of n-manifolds where we already know that one of them is an n-sphere. (Maybe it generalizes to what I said, though?)
Also, when I said "what you say is not technically true", I was being in a mathematically abstract mood, where I interpreted your drawing and video of silly putty as the best effort to realize 1-dimensional lines using real materials. Everything I said about figure 8s and thetas is only true about infinitely thin 1-dimensional figures. A nice thick 3-dimensional figure 8 and a nice thick theta are in fact homeomorphic.
The Poincare Conjecture still is cool, though :)
I put this on YouTube years ago but forgot to add the link to the original post: http://www.youtube.com/watch?v=8fvmP59953k
(just showing this to nagle now!)
Post a Comment